1. Bayesian Classifier
데이터를 일정 기준으로 분류 -> 데이터 중 어떤 것으로 분류되었는지 확률값을 알고싶다.

분류방법 : 확률값 높은 class 1로 분류


하지만 posterior 직접 못구함 -> 식을 바꿔서 구할 수 있는 애들로 구하자

prior ( 사전 )
자연에서 가져온 데이터로 traing data와 independent함
수집하기 전에 이미 확률 알고있음
충분한 데이터 없이 분류를 해야하는 경우 유용함

예시)

Likelihood ( 가능도 )
관찰데이터의 빈도를 나타냄
정규분포를 통해 구할 수 있다.

evidence
분류 결정에 영향x ( 분자로만 대소비교가능 )
posterior의 확률 분포를 얻고자 할떄 사용
모든 wi가 mutually independent하기 때문에 아래와 같이 식 변형 가능

posterior
prior과 likelyhood에 기반한 decision boundary를 가짐 -> 결정할 능력이 있다
데이터의 분포를 통해 ( 가능도 ) 바운더리 결정하기 때문에 현재의 관찰로만 결정 x -> 인간다운 결정

error
더 작은 확률이 결과로 나타나면 error

2. Parameter Estimation
gnerative : 모델링 결과로 데이터 일반화 가능 ( 분포 존재 )
discriminative : discriminative function을 찾는 것
parametric : 파라미터 최적화 ( 가오시안 분포 가정 )
non - parametric : 파라미터 x = 분포가정x
Discriminate function for decision boundary


두 함수의 교점 = decision boundary임
likelyhood가 가오시안 분포를 따른다고 가정함
Maximum Likelyhood Estimation
학습데이터로 주어진 확률함수를 최대로하는 파라미터를 추정
gnerative, parmetric한 접근
추정된 파마미터가 있지만 미지수
관찰데이터에 기반한 확률함수를 최대로해서 얻은 파라미터를 최선으로 여김
샘플수 증가 -> 추정이 좋은쪽으로 수렴
실제 데이터 분포 구하기 힘듬 => 가오시안 분포로 가정 => 평균, 분산 추정 => 가장 확률이 잘 맞으려면?

가 최대가 되는 파라미터를 구함

계산이 쉽게 log취함

미분해서 0되는 값 찾음

m 몰라

둘 다 몰라

정리
실제 데이터 분포 구하기 힘듬 => 가오시안 분포로 가정 => 평균, 분산(세타) 추정 => 가장 확률이 잘 맞으려면
우도함수 최대일 떄 => 미분해서 0찾아 => 뮤 모를 때, 시그마 모를 때, 뮤 시그마 둘 다 모를 떄 미분해서 구할 수
Navie Bayesian Classifier
다변량일 때 세타 추정 복합하고 시간 오래걸림

모든 feature을 mutually independent하게 조건

독립이므로 다차원의 평균과 공분산이 아닌 각각의 가오시안 분포의 평균과 분산을 구해 추정할 수 있다.

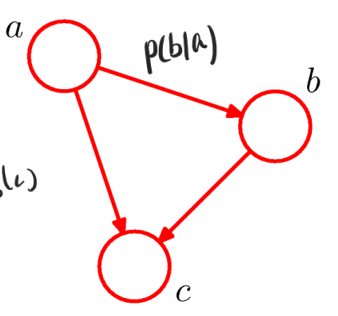
Bayesian Belief Network
독립적이라고 가정x인 경우 관계로 표현
노드 : feature, 간선 : 확률

'머신러닝' 카테고리의 다른 글
| 6장 Model Evaluation (1) | 2023.10.25 |
|---|---|
| 5장 Nearest Neighbor Method (0) | 2023.10.25 |
| 4장 Logistic Legression (0) | 2023.10.25 |
| 3장 Regression (1) | 2023.10.24 |
| 1장 Introdution to Machine Learning (0) | 2023.10.23 |


